A Machine Learning or Deep Learning model must be in balanced state (Generalized)
If you ever built a supervised Machine Learning model on some real-time data, it is impossible that it will perform well both on train set and test set in a first evaluation attempt. Real-time data is so noisy, of course as part of model building activity you might have performed enough cleanup and did efficient feature engineering, though usually the model either will tend to overfit or underfit the training data.
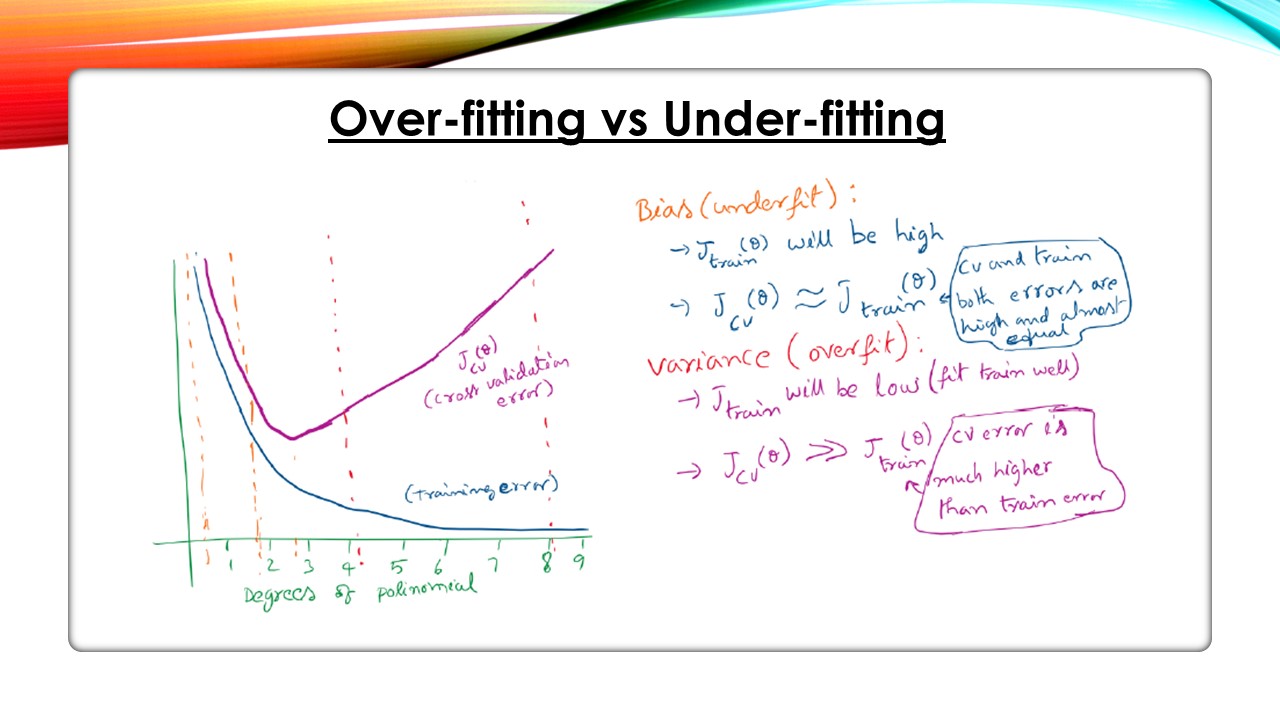
How do you detect if the model is underfit (Bias Problem) or overfit (Variance Problem)?
Usually between train set and test set, there can be a special sample of data which is called as cross-validation set. Out of couple of cross validation techniques like KFold CV and Bootstrapping, most of the times one may choose and apply K-Fold cross-validation technique over train set to gain a “cross validation set”.
In simple terms, when training happens – if the model is performing much better on train set but not performing well on cross-validation set, then you would say that the model is overfit. If the model is not performing well on train set itself, you would say that the model is underfit.
Underfit is considered as “High Bias” problem, Overfit is called as “High Variance” problem.
Here is an example for illustration:
| Performance on Trainset | Performance on Cross-validation set | Assessment Result |
| 88% | 75% | Overfit |
| 85% | 72% | Overfit |
| 85% | 82% | Ideal fit |
| 67% | 70% | Underfit |
| 65% | 58% | Underfit |
Why did the model Underfit? What are the next steps?
It’s because the model could not capture the underlaying data pattern well.
It may be because of the poor examples (records) or low contributing features in train data which don’t properly represent the real-world data. Better get a representative sample / (additional) features. However, note that, the data collection mechanism in this case can be a an expensive and time-consuming activity).
It may be because the data is non-linear, but you are trying to fit a linear model to the data. In this case choose a non-linear model. Other wise add polynomial features to the data and choose a complex model.
It may be because you regularized your model already and might have choose high lambda value. In this case you must shrink/decrease the regularization parameter (lambda) value.
In case of Deep Neural Networks, you may increase the number of layers.
Why did the model Overfit? What are the next steps?
It’s because the model could capture the patterns in the training data well including noise! it is like your model is memorizing all the patterns in your data unnecessarily and failing to generalize well to the new datapoints. That means the model is performing well on training data but making large errors on cross-validation data (or test data).
Usually over fitting is most common with non-parametric models (like DecisionTrees, RandomForests)
It may be because the data has very few training examples and many features (such as polynomial features), that’s why the model is overfit, hence collect more training examples (as you are aware collecting more examples can be an expensive and time consuming activity – decision on more data collection should be made after looking into learning curve), and reduce the number of features – try smaller sets of features.
ML Approaches to select smaller sets of features:
- Non-parametric models (such as Decision Tree) usually tend to over-fit. The ensemble models such as RandomForest, Bagging can be treated as a solution to reduce the over-fitting (n-number of models with random sub-sets of features). This can be achieved by tuning relevant hyper-parameters like min_features, max_features, max_depth, min_samples_split, min_samples_leaf, max_features with appropriate values (pruning). This will help to achieve a balanced model that performs both on train and test set well.
- For Parametric models, if we consider Linear Regression, Logistic Regression as examples, we can apply L1/L2 regularization. Model will reduce/increase coefficients when we tune shrinkage hyper-parameter. If a feature’s coefficient becomes zero, the feature is unimportant else, the feature has positive/negative effect on the prediction. The magnitude of coefficient determines feature’s importance. This regularization process will help model in adjusting coefficient values to fit best on Train and Test set. This way the over-fitting gets fixed. Please remember to scale (standardize / normalize) the features before applying regularization (especially before applying Gradient Descent solver).
- In case of Neural Networks, you may apply “drop out” technique, so that the network can generalize better.
When model is over-fit, the tools like GridsearchCV and RandomisedsearchCV provided in Scikit-Learn would help us tune hyper-parameters.
Bias – Variance tradeoff:
The interesting point is, Bias and Variance come together that means when you try generalizing an overfitted model it might reach underfit, and vice-versa. Hence you must tune the model such a way that it will balance well between reasonable Bias and Variance. In general, we try to overfit models and then finetune hyperparameters and balance the model.
Please reach us [email protected] in case you want more explanation and coding examples on bias vs variance.
-By
Praveen Vasari

I am forever thought about this, thanks for putting up.