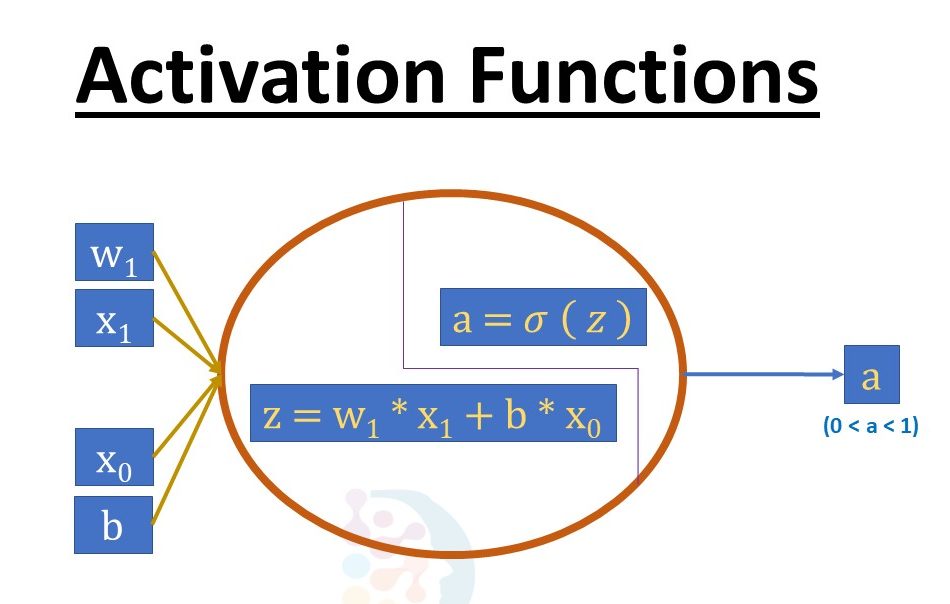
“Activation Functions” play a critical role in the architecture of Artificial Neural Networks (ANN).
The Deep neural networks are being successfully used in many emerging domains to solve real world complex problems. To achieve the state-of-the-art performances, the Deep Learning (DL) architectures use activation functions (AF’s), to perform diverse computations between the hidden layers and the output layers.
In order to relate with the context, let’s briefly talk about the basic architecture of ANN (Artificial Neural Networks).
- A neural network is typically composed of individual, interconnected units usually called neurons, nodes or units.
- The node or artificial neuron multiplies each of these inputs by a weight. Then it adds the multiplications and passes the sum to an activation function.

- The activation function therefore transforms the activation level of a unit (neuron) into an output signal.
What exactly does an Activation Function do?
Activation functions are mathematical equations that determine the output of a neural network. The function is attached to each neuron in the network and determines whether it should be activated (“fired up”) or not, based on whether each neuron’s input is relevant for the model’s prediction.
Activation functions determine the accuracy of Deep Learning model and also the computational efficiency of training a model that can make or break a large-scale neural network. Activation functions also have a major effect on the neural network’s ability to converge and the convergence speed.
Different types of Activation Functions:
Activation function can be either linear or non-linear depending on the function it represents.
1. Linear Function:
– It is a straight-line function where activation is proportional to input
(which is nothing but the weighted sum from neuron).
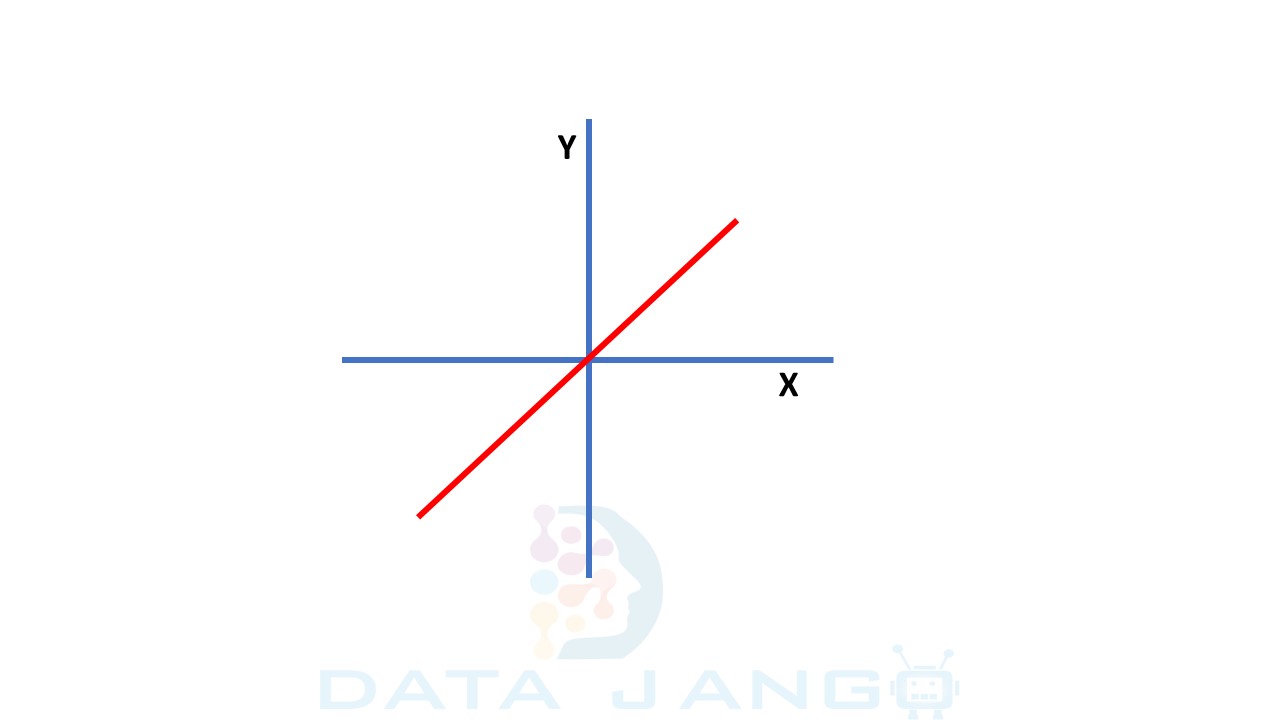
– It outputs a real value between range (-inf, inf), so it is not binary activation. Hence, never used as activation function for hidden layer nodes.
– Generally, we use linear activation function as output node (for regression as well as classification problems) in TensorFlow – Deep Learning models.
2. Non-Linear Function:
A. Sigmoid Function:
– The Sigmoid Activation Function is sometimes referred to as the logistic function.
– Sigmoid takes a one or more real values as input and outputs a number between 0 and 1 unlike Linear Function with values between (-infinity, + infinity).
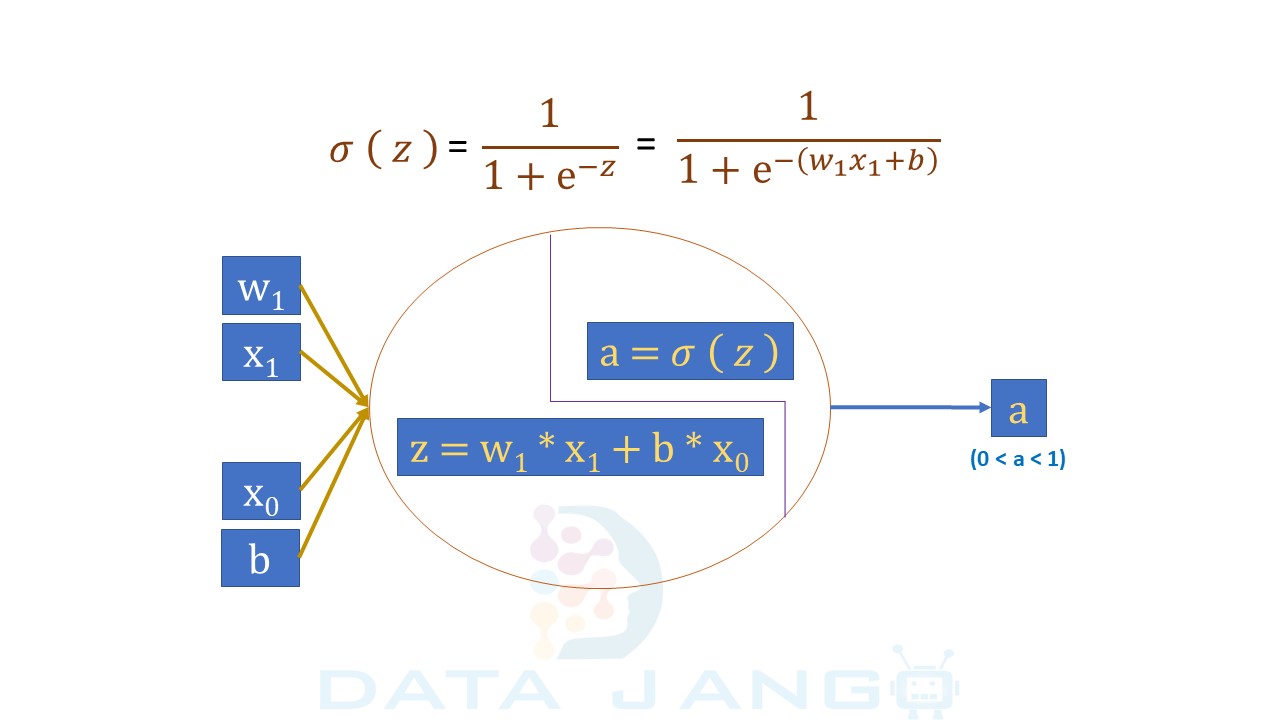
– It’s non-linear and has a fixed output range.
– It has a smooth gradient and suitable for Binary classification.
– The concern using this Activation Function is,
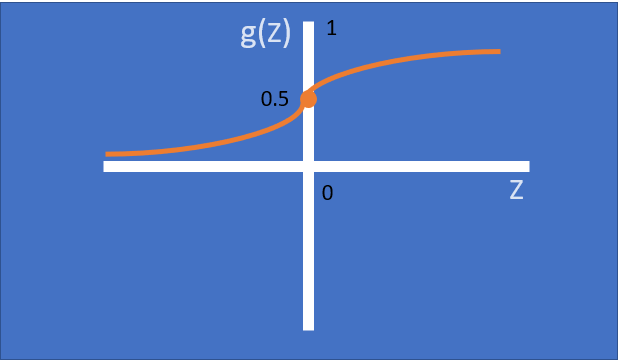
- Towards either end of the sigmoid function, the Y values tend to respond very less to changes in X.
- Sigmoid function may not be the best for some of the Use Cases because the slope/derivative of the activation function g(Z) is zero when the Z values are having bigger positive/negative numbers. This will lead to “Vanishing Gradients” problem.
- It is computationally expensive too.
B. Tanh Function:
– Tanh Activation Function is also non-linear and takes one or more real values as input and emits a number between [-1,1].
– Unlike Sigmoid, the output is zero centred (below figure) making it easier to model inputs that have neutral, strongly negative and positive values.
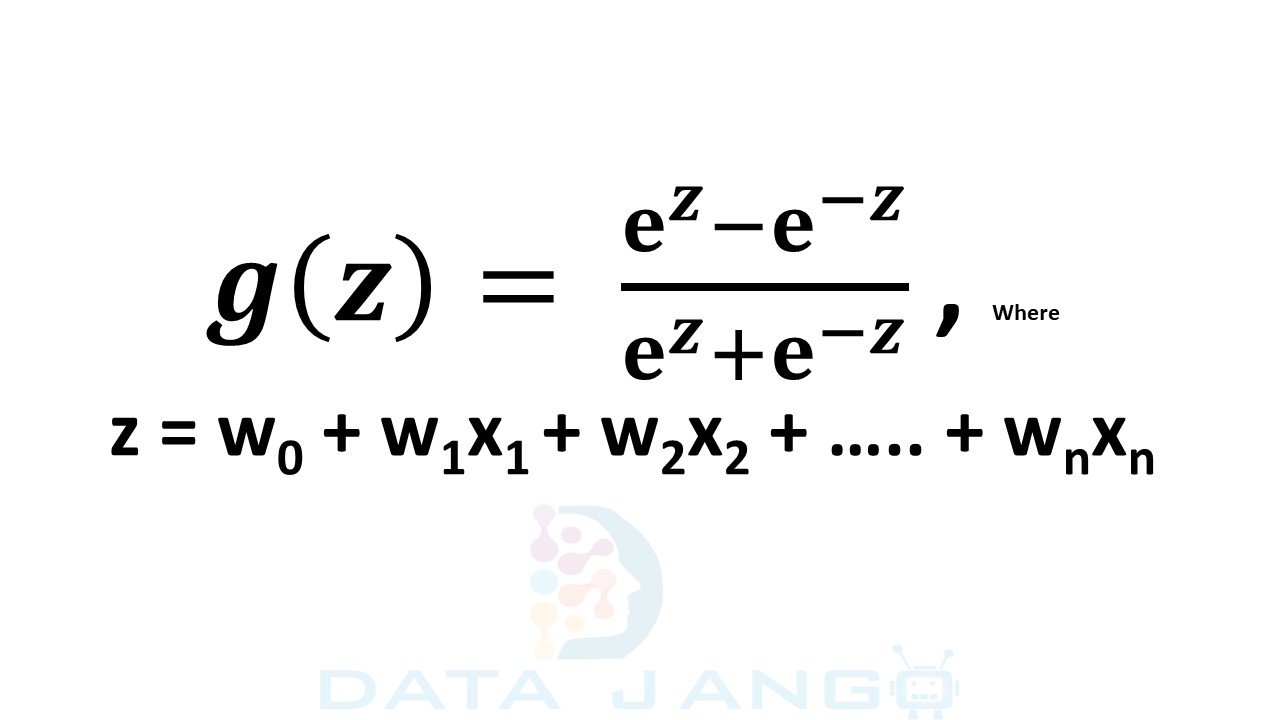
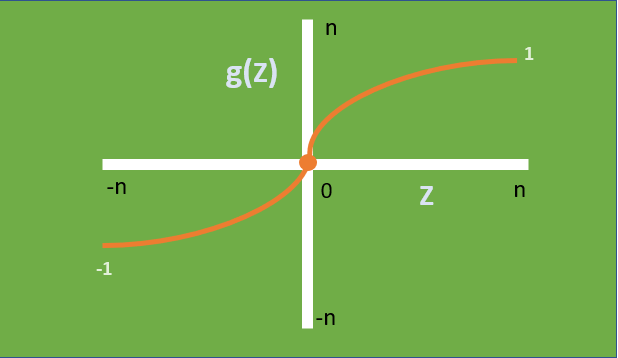
– The gradient is stronger when compared to Sigmoid (i.e. slope/derivatives are steeper).
– Tanh Activation Function suffers from “Vanishing Gradients” problem like Sigmoid function.
C. ReLU Function: (Rectified Linear Unit)
– ReLU Activation Function provides the same benefits as Sigmoid function but with better performance (i.e. computationally efficient by allowing the network to converge faster due to simpler mathematical operation).
– The idea is to rectify the “Vanishing Gradients” problem and thus ReLU was introduced.
– The output range of ReLU is “max (0,Z)”
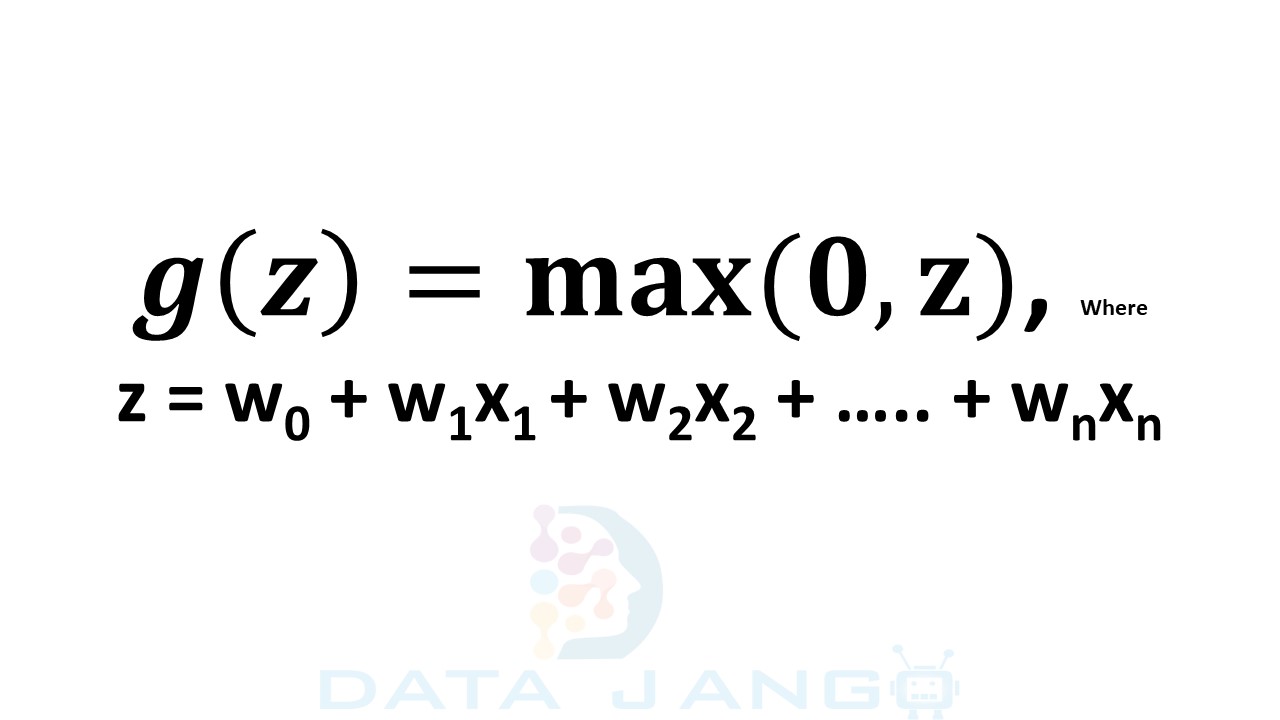
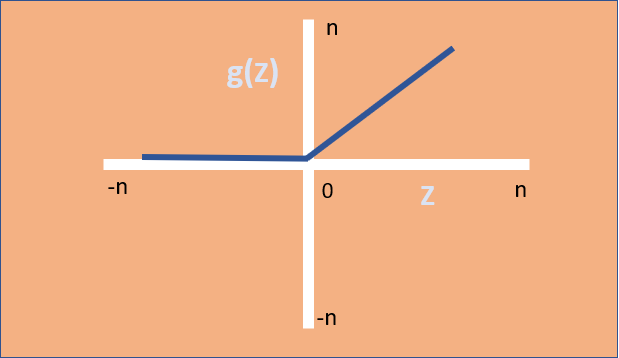
– One of the limitations is that ReLU activation function should only be used in the Hidden layers of the Neural Network.
– There could be a state of “Dead Neuron” (or) “Dying ReLU” problem where the neurons stop responding to the variations in the error/input. This happens because of the activations in the region (Z<0) of ReLU where the gradient becomes ‘0’ resulting to weights not getting adjusted during the descent and cannot perform “Back Propagation” (i.e. failure to learn).
D. Leaky ReLU Function:
– Leaky ReLU is most prominent activation function amongst others as it solves many use-cases that involve deep learning.
– To overcome the drawback while using “ReLU”, this variant of activation function was introduced.
– The variation has a small positive slope (ideally “0.01” – referred as ‘alpha’, typically a hyperparameter) in the negative region enabling backpropagation, even for negative input values (Z<0).

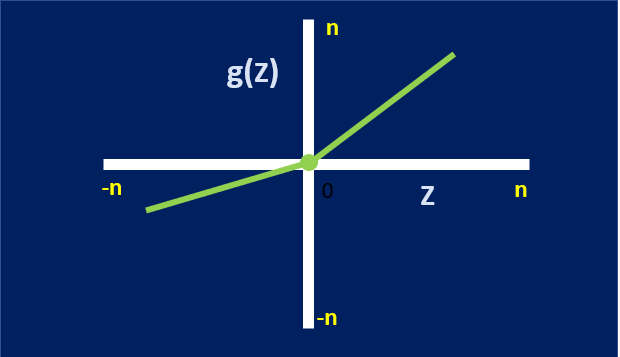
– The area of concern is that, Leaky ReLU activation function doesn’t provide consistent predictions for negative input values.
E. Softmax Function:
– The Logistic Regression model can be generalized to support multiple classes directly, without having to train and combine multiple binary classifiers. This is called “Softmax Regression”, or “Multinomial Logistic Regression”.
– When given a set of independent variables ‘X’, softmax regression model first calculates logits for each class – k.
– Once you have computed the score of every class for the instance x, you can estimate the probability k that the instance belongs to class k by running the scores through the softmax function as it computes the exponential of every score, then normalizes them (dividing by the sum of all the exponentials).
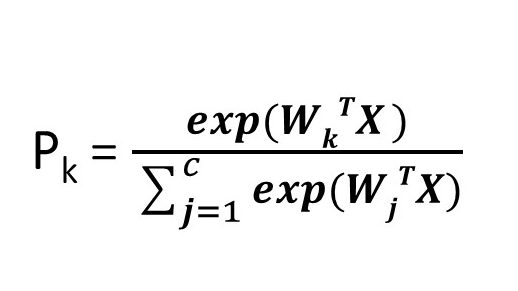
– Maximum value that we get out of all K classes will give us the maximum probability which will be considered as the final class.
3. Variants of existing Activation Functions:
F. Parametric RELU Function:
– This AF allows the usage of a hyperparameter ‘alpha’ unlike “Leaky ReLU” where this value is fixed.
– The ‘alpha’ is passed as an argument and helps learn the most appropriate value (during negative slope) while performing backpropagation.
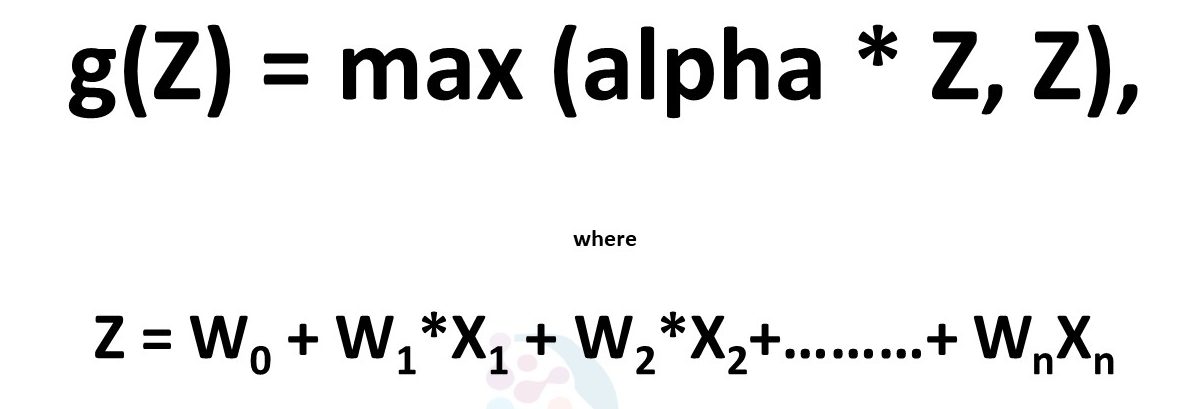
G. SWISH Function:
– This is a newly experimented AF that tends to work better than ReLU with similar computational efficiency across multiple challenging datasets.
– The simplicity of Swish and its similarity to ReLU make it easy for practitioners to replace ReLUs with Swish units in any neural network.
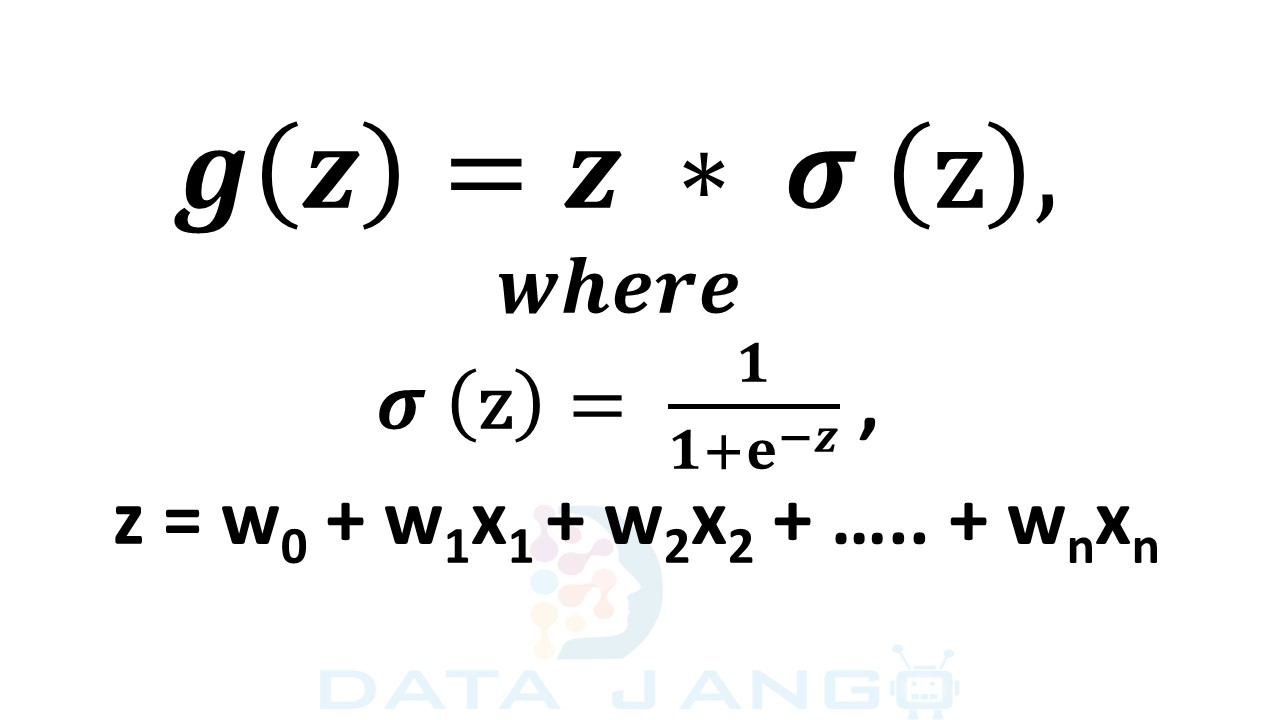
Conclusion:
– There is no one best “Activation Function” that works for all problems, sometime we have to end up trying (Cross Validation) multiple functions and select the best.
– The hidden layers should always have “Non-Linear Activation Functions”, otherwise it is equivalent to have one linear function irrespective number of layers and nodes.
-By
Venkat Challa

Good information. Lucky me I found your blog by accident (stumbleupon). I have saved it for later!|